-
POKEing to the Commodore 64 screen
I was looking through the Commodore 64 Programmer’s Reference Guide, in the chapter about graphics, how I could POKE screen codes to the screen, so to speak, in 6502 assembly. Here is what I came up with.
First of all, what do I mean with “POKE” and “screen codes”?
POKE is a CBM Basic 2.0 command, also available on many Microsoft Basic variants on 1980’s and 1990’s home computers. It allowed the programmer to place a value anywhere in the 64 Kb of memory addressing space available to the Central Processing Unit (CPU, which is the 6510, a variant of the 6502). Since the screen in the default configuration is located at memory addresses 1024 to 2023, one could put a value A into column C and row R as follows:
POKE 1024 + 40*R + C, Awhere:
0 <= R <= 240 <= C <= 390 <= A <= 255
This is all well and good, but it seems rather slow, even if we invoked these commands in 6502 machine code. I’ll come to that later.
Screen codes are Commodore specific values, which are used internally to represent characters. There is a direct correlation between a screen code an its position in the character ROM. The codes are different than the codes used for printing (which codes are collectively called PETSCII, Commodore’s own version of ASCII). For instance the letter ‘A’ is the value 1 in screen code and 65 in PETSCII.
Why do I even want to POKE screen codes to the screen, if the same can be done using PETSCII and printing? Well, I want to put blocks of screen codes onto screen, using a self-defined character set, to use for a video game. In that case the Basic commands and even the routines in the underlying operating system (Kernal) are just too slow. I need custom routines to put screencodes onto screen.
So I started to explore what is needed.
It seems the video chip, the VIC II, can only “see” a quarter of the 64 Kb of addressing space, i.e. 16 Kb, in four banks:
- bank 0, $0000 - $3FFF (default)
- bank 1, $4000 - $7FFF
- bank 2, $8000 - $BFFF
- bank 3, $C000 - $FFFF
This is controlled through bits 0 and 1 of data register A (DRA) of the Complex Interface Adapter (CIA) chip. There are four possible values:
- %11 VIC II bank 0 (default)
- %10 VIC II bank 1
- %01 VIC II bank 2
- %00 VIC II bank 3
So bits 0 and 1 have to be inverted to get the binary value of the VIC II bank. Furthermore, in order to read data register A, their bits have to be set to zero selectively in the data direction register (DDRA) for data register A. All the other bits of DDRA have to left alone.
Within the 16 Kb available at one time to the VIC II, there are 16 possible relative locations of screen memory (25 lines of 40 characters, or 1000 bytes):
- $0000 - $03E7
- $0400 - $07E7 (default)
- $0800 - $0BE7
- $0C00 - $0FE7
- $1000 - $13E7
- $1400 - $17E7
- $1800 - $1BE7
- $1C00 - $1FE7
- $2000 - $23E7
- $2400 - $27E7
- $2800 - $2BE7
- $2C00 - $2FE7
- $3000 - $33E7
- $3400 - $37E7
- $3800 - $3BE7
- $3C00 - $3FE7
The relative base address of screen memory is controlled by the lower 4 bits of register 24 of the VIC II. Again, only these bits should be manipulated, while the upper 4 bits should not be changed for selecting the screen location. Of course, I am only reading the bits, so I’m safe in that regard.
The Kernal has (half) a pointer to the full address of the beginning of screen memory, the high-byte. This pointer is stored in location 648 ($288). I can either use that, or calculate it myself.
- $288 (648): high-byte of pointer to the base of screen memory
Of course, if I would relocate the screen, I would have to change this pointer in my code, so there’s value in knowing how to calculate this high-byte, even if it isn’t needed if I don’t change the screen location in memory. I could just as well use the value in $288.
I calculated the high-byte of this pointer as follows:
; some addresses defined vicmemptr eqm $d018 ; VIC II memory pointer register cia2rega eqm $dd00 ; CIA 2 register A cia2ddra eqm $dd02 ; CIA 2 data direction register A ; determine location of screen memory ; returns .A hi byte of base address of screen memory ; modifies .A, flags screenbas: ; determine the VIC II base address lda cia2ddra ; set and #%11111100 ; bits 0, 1 sta cia2ddra ; of reg A to "read" lda cia2rega ; read reg A and #%00000011 ; only bits 0, 1 eor #%00000011 ; invert bits 0, 1 lsr ; optimization -> shift into bits 6, 7 ror ; in effect, multiply by 2^6 sta screenb1+1 ; self-mod code ; determine location of screen memory inside the 16 Kb VIC II bank lda vicmemptr ; get and #%11110000 ; upper 4 bits lsr ror ; make it hi byte * 2^2 ; add base address of VIC II to relative base address of screen memory clc screenb1: adc #$ff ; self-modded rtsI hope you didn’t mind my code self-modification trick, but it does work in RAM. In ROM one would do it differently, naturally.
Now I know where the screen is located in memory, how can I put a screen code into a particular column and row? There are 40 columns and 25 rows, numbered from 0 to 39, and to 25, respectively. This means the memory location, based on column and row value can be calculated as follows:
- screen base + column * 40 + row
I’ll use indirect indexing to point to this address, where the .Y register serves as the index:
sta (putadr),y ; store it in the yth columnwhere
putadrholds the address of the first row of the column on screen. The .Y register then accesses the Y-th column in the instruction above. It makes sense to store the column value in the .Y register (the same as the Kernal does).Adding address values is pretty straight forward, but how to calculate times forty?
Remember that the 6502 has a shift left instruction, which is equivalent to multiplying by two. So, with some shifting and adding it is possible to get to times forty quicker than doing it traditionally (multiply two 8-bit values into a 16-bit value):
value * 40 = ( value + (value * 2^2) ) * 2^3
That is 5 left shifts and 2 additions. However, while five times a column value still fits into a single byte, multiplying it by 8 doesn’t fit in that single byte anymore. At that point two bytes are needed.
Here is the code:
; put screen code onto screen ; parameters: ; .A screen code ; .Y screen column, between 0 and 39 ; .X screen row, between 0 and 24 ; returns: ; carry flag set means an error occurred ; all registers are affected ; bits 0, 1 of DDRA of CIA 2 ($DD02) are set to zero (read) ; zero page $02, $03 are used putadr: eqm $02 ; 2-byte screen address putonscn: cpy #40 ; column >= 40 ? bcs putexit ; yes, then exit w/ error cpx #25 ; row >= 25 ? bcs putexit ; yes, then exit w/ error pha ; save for later stx putadr ; initialyze screen address txa ; transfer row to .A asl asl ; row * 2^2 adc putadr ; row * 2^2 + row sta putadr ldx # 0 ; zero hi byte stx putadr+1 ; of screen address asl rol putadr+1 asl rol putadr+1 asl rol putadr+1 sta putadr ; (row * 5) * 2^3 jsr screenbas ; add hi byte of screen base address adc putadr+1 sta putadr+1 ; baseadr + (row * 40) pla ; get screen code back sta (putadr),y ; store it in the yth column clc ; no errors putexit rtsTo check if this code actually works I added a combination of assembly and Basic language, so it could run from the Basic prompt on the Commodore 64 with the RUN command.
It working made me a happy coder.
-
On the C64, using the Kernal, you can set the cursor position (one routine) and then print a character (another routine). I wanted a single routine to put a screen code onto the screen, at a particular colomn and row, wherever the screen was located in memory. So I wrote it, and it works, yay! 👨💻
-
I installed droid64, a Java application to manipulate Commodore disk images and copy files between your host OS and a disk image (e.g. a file with a D64 extension). I needed it to be able to play new games. I also put a SPEEDLINK SL-650212-BKRD Competition PRO USB joystick on my Amazon wish list 🎮
-
Challenge the challenger (or: a little help wanted here)
It is said, by some, that there’s nothing magical about January 1. So resolutions seem rather nonsensical, at least, putting a start date on something. Just start, which is what I just did, by writing and publishing this blog post. And, I warn you in advance, I will ramble and meander through my “ideascape” (if that’s even a word—it now is).
As announced in my previous post, and I’m still calling it that, my self-challenge is called 366 Days of Coding. The year 2024 will become the year that I finally produced a video game. I’ve tried many times before, but was held back by lack of confidence, mostly. I’ve worked on that in 2023, and my improved mental hygiene should give me the protection against self-doubt I need.

Now how is this going to work, what will be my general overarching workflow? Well, I don’t know… I’ve never been much of a planner. I always let deadlines pass by, and brushed it off as proof that I’m worthless, because, well, see! That’s no way to live. First of all, seeing how long indie games are in beta, testing and debugging seems a rather important part of software development. Also, it’s good to have a second opinion to rely on, which means beta-testers. However, on my first try I’ll have to do most of that myself, since I lack any reputation to call for outside help, and actually receive help.
I can imagine it’s like writing one’s first novel. It takes such a long time, because a lot has to be learned, especially accepting outside help from a closed reader group, who give positive feedback on one’s writing. In that first attempt, as a new writer, I guess most figure that out for themselves, perhaps by using a partner or close friends as “guinea pigs”, or whatever is available to them. Purposefully looking for a group of dedicated beta-readers, often means one has been oneself first. I suppose being an avid reader is a prerequisite for becoming a writer, why else would one even want to write a book? In fact, helping a writer out with positive critique may give the critic ideas on how to become a writer themselve. From that perspepctive, gathering a group of beta-readers seems to me like paying something forward, from the writer’s point of view.
However, there are many more readers of books than there are players of retro-games. It’s a self-selecting group of mostly older people with nostalgia, and younger people who can identify with the old times, as an esthetic. They will be opinionated, perhaps even rude, since they are far off the beaten path, into a barren land (space-time, actually) that once was great and thriving, and only is accessible through personal memory and documentation (books, magazines, videos, etc.). On the other hand, retro-gaming is having a revival, as all things eighties of the previous century. Things in the current news are rather grim, and there is certainly a hunkering for the good old days, even in those who never lived through those.
So, however I will go about things, testers are an essential part of software development. After all, a video game, like a book, is to be experienced by others than the author/creator. It makes sense to accept input by those others, not what or how to make something, but how they experienced what you made. Still, there are always those who think they know better than you, and offer how-to tips. They might know better, but you are the person making, on your terms, schedule and responsibility. Whatever you make, it is always a compromise between what you aim at (aim as high as you can), how much time you have (besides daily chores, work, etc.), and what you can put up with and still enjoy it (mostly).
If you have no idea of the final product, don’t have the time, and don’t like the process, this is not for you.
I have some ideas what to make, so many, that I need to pick one. My first task, then, is to explore the world of indie gaming on retro computers, briefly (!), and see what I like and don’t like. There are no original ideas—well so few that they don’t stand out—but there are original spins on existing ideas. With a shortlist of ideas I can think about what my take would be. This will lead to an opinionated product, some will like, others won’t. That is a good thing, since you don’t want a bland product no one hates, but also no one prefers. You can’t please everyone. Heck, it’s hard to please anyone nowadays, with the world being as polarized as it currently is.
After having a list of possible ideas, it’s time to prototype, and see what appeals to me. This is often done on paper or in a design document, rough, yet playable, if you do the mechanics of the game yourself. In the final game this is all automated, but in this rough stage, you are the driver, leaving room to change mechanics on the fly.
Now comes the hard part, picking and committing. You can always go back and pick something else once you hit a dead end, but that shouldn’t be par for the course.
What comes after that is still blurry to me, because I’ve never done something like this before. I’m sure to keep you posted once I discover the intricacies of game development, at least, how I perceive those. This is an experiment of one. You shouldn’t copy someone else’s workflow, but, instead, learn from it, to improve yours. This doubly applies to a newbie like myself, looking at how other, more seasoned developers go about things.
It will be educational. Of that I’m sure.
Thanks for sticking with it until the end of this thought piece. I’m sure I got most things (slightly) wrong. Please feel free to comment and enlighten me with your bright ideas, maybe suggest (parts of) how to do what I’m planning to do. I’m sure I will learn something from it, and, reciprocally, by formulating your ideas in clear words, you might as well.
-
I redid the random maze program in assembly language. If you load and RUN the program, it displays the maze, waits for the user to press a key, then clears the screen and returns to the BASIC prompt. It’s simple, but it made me proud nonetheless that it actually works.

-
I have found a better way to assemble 6502 code than Virtual 6502 Assembler. I installed DASM from the official Pi OS repository on my Raspberry Pi-400, rewrote the KickAss source code, and assembled that into a BASIC loader program. Took long, because of differing assembler directives, and a nasty typo 🤬
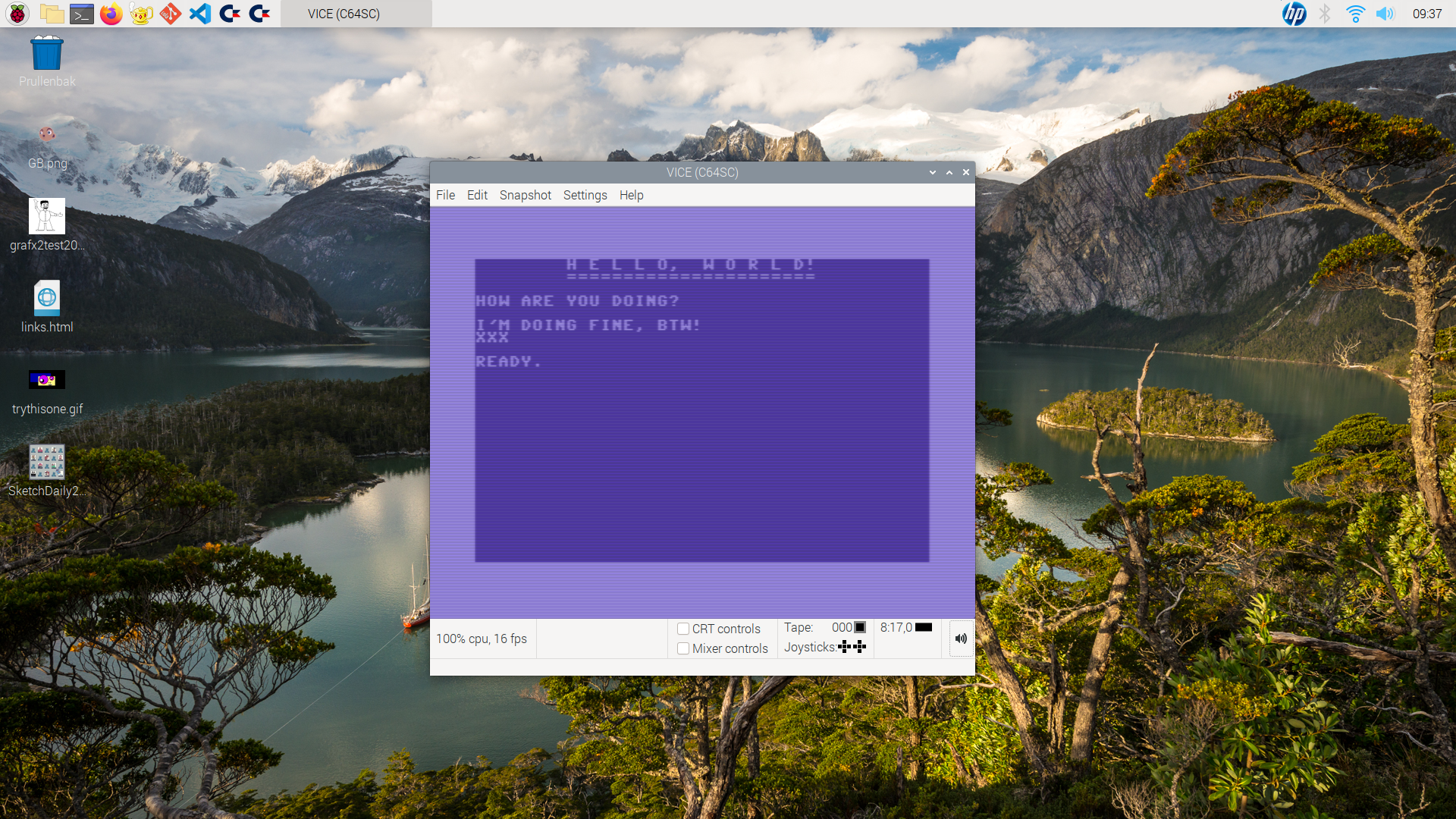
-
Getting a foothold into 6502 machine language, bonus part
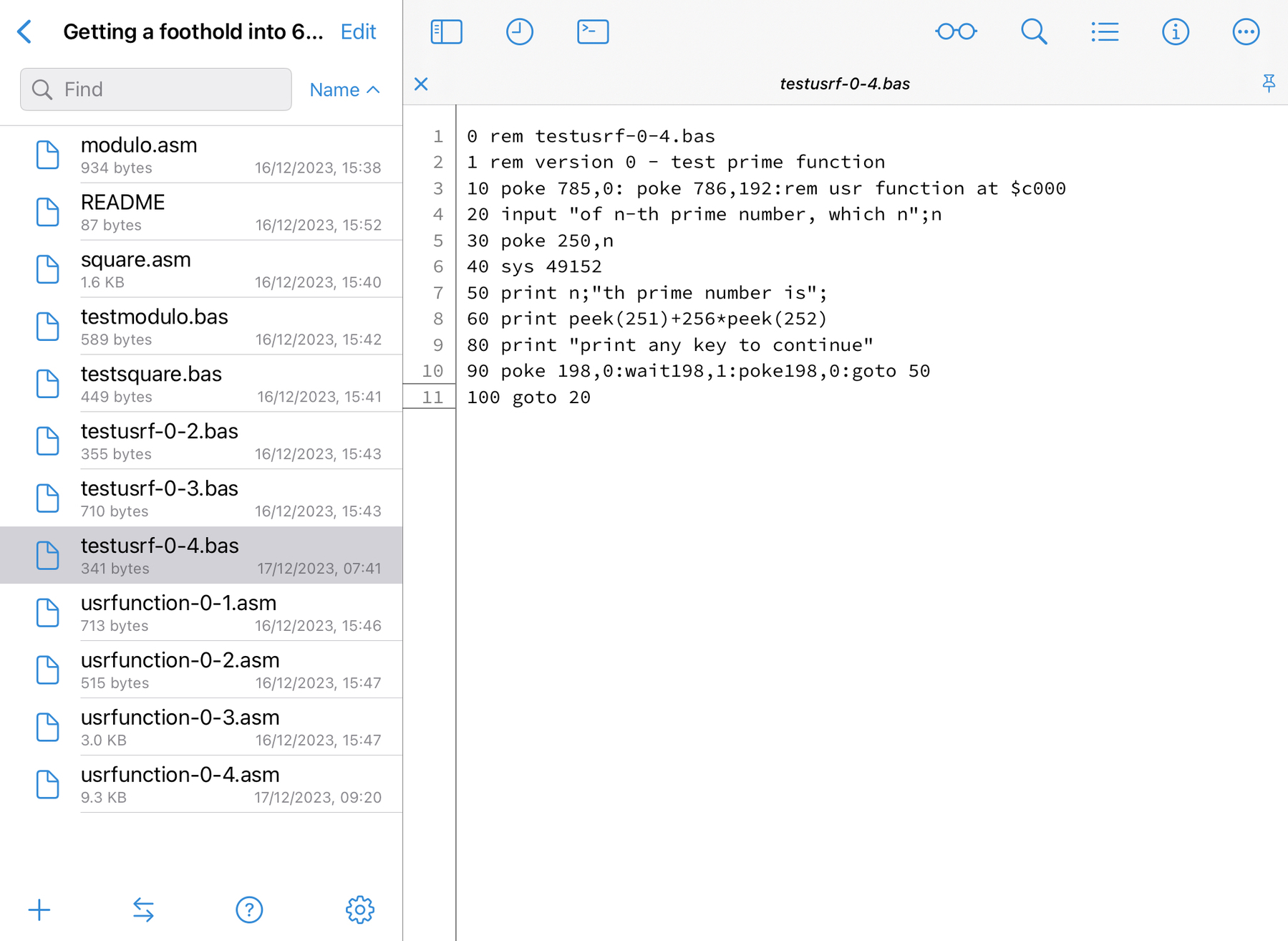
The file I assembled and downloaded as a .PRG file, using the Virtual 6502 Assembler, I smart attached in the V.I.C.E. C128 emulator. I then attached an empty .D64 disk file, and used Basic 7.0 to save memory location $C000 to $C12F to a binary file, called “usrfunc04.c000”. I detached the .D64 file, and closed V.I.C.E. C128. In the C64 emulator I rewrote the previous C64 Basic program so it loads this binary file from disk. It then proceeds to checking of primality of numbers between 0 and 65535. I saved this Basic program to the same disk as the binary file, and copied it as text in the listing below.
[ part 1 | part 2 | part 3 | part 4 | part 5 ]
It was a bit of a hassle, but it all works, and that’s what counts here.
0 rem testusrf-0-4.bas 1 rem version 6 - test completed usr function 10 on s goto 20,40 20 print "loading binary file...":print 30 s=2:load"usrfunc04.c000",8,1 40 poke 785,0: poke 786,192:rem usr function at $c000 50 print "... (tests between 0 and 65535)":print 60 for n=0 to 65535 70 m = usr(n) 80 print n;"is ";: if not m then print "not "; 90 print "prime" 100 print "any key to continue" 110 poke 198,0:wait198,1:poke198,0 120 next n -
I had to search for a particular Commodore 128 command, and found it here, which, BTW, I typed in myself from a book, and corrected many errors in that book. It now is the definitive guide on the web for Commodore 128 retro-computer users. It is anonymous, though, since I haven’t written the book.
-
Goal for 2024, making games for the Commodore 64
In the Commodore 64 Programmer’s Reference Guide, published by Commodore Business Machines, Inc. and Howard W. Sams & Co., Inc. in 1982, there is a chapter on programming graphics with history’s most popular retro-computer. Graphics are an essential part of computing, and understanding how it works under the hood is essential for the C64, since it has no Basic commands to manipulate graphics. It all has to be done with PEEKs and POKEs.
I want to use C64 graphics to create a simple game, maybe a few games. There are a few characteristics to a video game:
- introduction screen (typically colored bitmap graphics) while loading the code and assets
- game area, which has to be somewhat fast, which rules out bitmap graphics, instead what’s mostly used is:
- standard character mode with programmable characters for black and white games
- multi-color character mode with programmable characters for color games
Modes can be mixed, using interrupts when the electron beam isn’t displaying anything. Of course, this is an advanced programming technique, and doesn’t always render perfectly.
On top of that there are hardware sprites, all 8 of them, but those can be multiplied virtually, by moving them lower on the screen after they have been displayed by the VIC-II chip. It all comes down to timing, and, hence, using optimized 6502 machine language. Sprites, since they are moving, can bump into each other, which is only possible doing convincingly using machine code. It seems all very exciting and challenging.
If the world of the game is larger than what fits on a video screen, side scrolling can be used. Side scrolling is a video game genre in its own right. There’s also free scrolling, where the screen is a window on the game world that can move up, down, left and right.
Since there is a limited amount of memory in the computer, it makes sense to use repeating patterns to represent the game world. The screen then exists of tiles of the same content, which together represent grass, forest, pavement, etc. It is part of game design.
The game logic could be written in Basic, though, since it doesn’t have to be so snappy, responding to user input. This also allows users to modify the game, which is a bonus, in my opinion. However, in order for Basic to work, RAM becomes inaccessible while Basic and Kernal ROM is being switched on, to enable Basic to run. There are ways around this, since, while switched away, RAM is still available, can even be written to, just not read from (and not be used while a Basic program runs).
The thing is, that the Commodore 64 is a very quirky computer, with many restrictions, that can be worked around, but need special attention from the coder, in other words, creative solutions.
To not get bogged down by details, maybe it’s more effective to start simple, and only make things more complicated if there’s a need for it. It’s better to write a minimal viable solution than keep putting off finishing, because it could be “so much more awesome.” Yes, it would, but will it ever see the light of day? Like real artists, real software developers ship.
Even games written in Basic can be quite appealing. Sometimes Basic isn’t fast enough, and in those cases one can use some machine language to speed things up. Games completely written in 6502 assembly language are often developed on another computer. Nowadays that would be a Mac or Windows computer.
The idea that the game player can change things appeals to me. Of course, that needn’t be in Basic. There are other programming languages. A popular one nowadays is Lua (free and open source, easy to implement in your own code). However, Basic is already there, so why not use it?
This is going to be a long haul, isn’t it?
Since it probably is, it would be such a nice goal for the end of 2024 to have developed and published a game for the Commodore 64, one I feel proud of.
Who knows, it might even be several games. For now, being realistic, let me stick to promising that I will finish at least one game.
However the gaming dice will roll for me, 2024 will be my “266 days of coding.” Yep, it’s a leap year.
-
Oh wow! I went to Github.com on my iPad, clicked on one of my repo’s, connected an USB keyboard and pressed the period key “.” 🤯
-
Doing the work, needing the tool (read: iPad Air, perhaps?)
Here’s an exercise from the book “Programming the 6502”, 4th edition, by Rodnay Zaks.
Exercise 1.12: Complete the following additions. Indicate the result, the carry C, the overflow V, and whether the result is correct or not:
10111111 (_______) 11000001 (_______) ------------------ ﹢ ________ (_______) V:____ C:____ [ ] CORRECT [ ] ERROR11111010 (_______) 11111001 (_______) ------------------ ﹢ ________ (_______) V:____ C:____ [ ] CORRECT [ ] ERROR00010000 (_______) 01000000 (_______) ------------------ ﹢ ________ (_______) V:____ C:____ [ ] CORRECT [ ] ERROR01111110 (_______) 00101010 (_______) ------------------ ﹢ ________ (_______) V:____ C:____ [ ] CORRECT [ ] ERRORTo say that this was easy to transcode in Markdown/HTML would be a grand understatement. My “code editor”, the Drafts app was fighting me all the way, and, while split view was showing me the PDF of the book in the Documents app, Apple’s native Files app was having a grand mal. So much so, that I had to reboot my iPad to get the Files app unjammed (it was completely locked up, unresponsive, frozen). I guess the 9th generation iPad isn’t cut out to do any “professional” work, like code-editing HTML 😅
I suppose if there was ever a reason to need a more pro version of the iPad, here it is. I guess an iPad Air would do much better, even if it costs twice as much as the “primary school iPad”—cough—iPad 9th generation.
I have a Raspberry Pi-400, but it has drawbacks as well, a gleaming one being lack of any good application software. Linux on the desktop is always “just a year away”, permanently 😉
I’m told 2024 will be “the year of the iPad.” I’m hoping it is, because not only is my current iPad underpowered, its battery also is getting old. You see, I’m not using it casually, as a beginner iPad user, but as a full-fledged work computer, so to say. In a school setting it would’ve been replaced, no doubt, or, at least, sent to an authorized Apple Service Center for maintenance & repair.
So, yay for 2024, may it bring me a nicer iPad.
🙄 I’m such a consumer, totally in the Apple camp of things…
-
Getting a foothold into 6502 machine language, part 5
I’ve rewritten the code I developed earlier and extended it into a full-fledged
usrmachine language routine. However, it needed testing, because of all the rewrites. So I grabbed my copy of Working Copy on my iPad and started Git-versioning both the assembly and the Basic code. It was invaluable for getting the code to work correctly.[ part 1 | part 2 | part 3 | part 4 | bonus ]
Here are some of the major changes I made:
- the input and output of functions now use the .A, .X and .Y registers
- the prime function now picks out of a list of all the 54 prime numbers that smaller than 256
- a main routine was added that tests the primality of the value put into the
usrfunction in Basic, and returns either a zero (false) or minus one (true)
After every part was tested, I ended up with a collection of documents, I’ll share next. These are the algorithm, assembly code, and Basic test program (the machine code already loaded in locations $c000, or 49152, and higher). I did away with a machine code loader in data statements, because that became too much of a chore. The point of this whole exercise was to learn something about coding for the Commodore 64, particularly in 6502 assembly language.
And that I have accomplished. It isn’t the most efficient 6502 machine language routine, but it does work. And that always makes me happy 😃
"algorithm.txt"main routine:
- convert the real number from Basic into a 16-bit unsigned integer, called “testnum”
- set primality flag to “false”
- for each of the 54 prime numbers that are less than 256,
- if (testnum == prime) then set primality flag to “true”, and go to step 6
- set primality flag to “true”
- for every next prime, starting with the 0th,
- if ( (prime * prime) == testnum) then set primality flag to “false”, and go to step 6
- if ( (prime * prime) > testnum ) then go to step 6
- if ( (testnum modulo prime) == 0) then set primality flag to “false”, and go to step 6
- convert the primality flag into a real value and return it to Basic
prime function:
- pick the n-th element out of a list of 54 primes, where n starts from zero, up to 53
square function:
- start with a zero value for the 16-bit square
- shift square 8 times to the left, and each time
- shift the 8-bit number to be squared left into the carry bit
- if there’s a carry, then add the original value of number to square
modulo function:
- shift the 16-bit dividend 16 times into the 16-bit remainder, and each time
- after each shift, test subtract divisor from remainder, and only store in remainder for positive values
"usrfunction-0-4.asm" ; usrfunction-0-4.asm getadr = $b7f7 givayf = $b391 *= $c000 jsr getadr ; convert real into unsigned int ; in .A & .Y (hi/lo) sty testnum ; save for later use sta testnum+1 ldx #$00 stx isprime ; assume it is not a prime cpy #$02 ; is testnum less than 2? lda testnum+1 sbc #$00 bcs okay ; testnum >= 2 jmp foundit ; no, then output value of isprime okay: ; test if test number is equal to one of the prime numbers ldx #53 stx order ; start with 53th prime loop1: ldx order bmi loop1x ; if < 0 then exit loop jsr prime ; get nth prime in .X cpx testnum ; is testnum == prime? bne loop1a ; no, then next prime lda testnum+1 bne loop1a ldy #$ff ; yes, then sty isprime ; it is a prime bne foundit ; skip to the end loop1a: dec order ; try previous prime clc bcc loop1 ; continue loop loop1x: lda #$ff sta isprime ; assume testnum is prime lda #$00 sta order ; start with 0th prime loop2: ldx order jsr prime ; find the nth prime stx temp ; store for later use txa jsr square ; square the prime cmp testnum ; prime * prime == testnum ? bne loop2a cpy testnum+1 bne loop2a ldy #$00 sty isprime ; yes, then it is not a prime beq foundit loop2a: cmp testnum ; is prime * prime > testnum? tya sbc testnum+1 bcs foundit ; then exit the loop ldx temp ; prime is divisor lda testnum ; testnum is dividend ldy testnum+1 jsr modulo cmp #$00 ; is remainder zero? bne loop2b ; no, then next prime cpy #$00 bne loop2b ldy #$00 ; yes, then sty isprime ; it is not a prime beq foundit loop2b: inc order ; try next prime clc bcc loop2 ; continue loop foundit: lda isprime ; primality flag is tay ; either $0000 or $ffff jmp givayf ; make it real & return to Basic testnum: .word $ffff ; container for number to be tested order: .byte $ff ; container for n, as in nth prime isprime: .byte $ff ; container for flag that signals ; primality temp .byte $ff ; temporary storage for prime ; prime ; Finds the nth prime on the number line. ; E.g. prime(0) = 2, prime(1) = 3, etc. ; ; input .X order n ; ; output .X nth prime number ; ; effects on .A, .X, .M, .Z prime: lda primes,x ; load from list of primes tax ; put it in .X rts ; ordered list of all 54 prime numbers less than 256 primes .byte 2, 3, 5, 7, 11 .byte 13, 17, 19, 23, 29 .byte 31, 37, 41, 43, 47 .byte 53, 59, 61, 67, 71 .byte 73, 79, 83, 89, 97 .byte 101, 103, 107, 109, 113 .byte 127, 131, 137, 139, 149 .byte 151, 157, 163, 167, 173 .byte 179, 181, 191, 193, 197 .byte 199, 211, 223, 227, 229 .byte 233, 239, 241, 251 ; square ; Calculates the 16-bit unsigned square of an 8-bit unsigned integer. ; ; input .A number to be squared ; output .A, .Y squared number (lo/hi) ; ; Destroys all registers. number = $61 ; 8-bit value to be squared nsquare = $62 ; 16-bit value of squared number tnumber = $64 ; temporary storage for number square: sta number ; put .A in number lda #$00 ; clear A sta nsquare ; clear square low byte ; (no need to clear the high byte, ; it gets shifted out) lda number ; get number in .A sta tnumber ; save original for later use ldx #$08 ; 8 bits to process sqloop: asl nsquare ; shift square to left rol nsquare+1 ; (i.e. multiply by 2) asl a ; get next highest bit of number bcc sqnoadd ; don't do add if carry is zero tay ; save .A for later use clc lda tnumber ; add original number value adc nsquare ; to square sta nsquare lda #$00 ; add a possible carry adc nsquare+1 ; to the high byte of square sta nsquare+1 tya ; get .A back sqnoadd: dex ; decrement bit counter bne sqloop ; go do next bit lda nsquare ; lo byte of square in .A ldy nsquare+1 ; hi byte of square in .Y rts ; modulo ; Calculate the modulo of an 8-bit number with a 16-bit number. ; ; input .A, .Y dividend ; .X divisor ; ; output .A, .Y remainder ; ; Destroys all registers. num1 = $61 ; 16-bit dividend num2 = $63 ; 8-bit divisor rem = $64 ; 16-bit remainder modulo: sta num1 ; .A lo byte of dividend sty num1+1 ; .Y hi byte of dividend stx num2 ; .X divisor lda #$00 ; clear remainder sta rem sta rem+1 ldx #16 ; do 16 bits modloop: asl num1 ; shift num1 to the left rol num1+1 rol rem ; into remainder rol rem+1 sec lda rem ; do trial subtraction sbc num2 ; with divisor tay lda rem+1 sbc #$00 ; divisor is 8-bit value bcc modnosub ; was there a borrow, ; then skip subtraction sta rem+1 ; save the result sty rem modnosub: dex ; repeat for 16 bits bne modloop lda rem ; lo byte of remainder in .A ldy rem+1 ; hi byte of remainder in .Y rts"testusrf-0-4.bas" 0 rem testusrf-0-4.bas 1 rem version 5 - test completed usr function 10 poke 785,0: poke 786,192:rem usr function at $c000 20 input "number";n 30 m = usr(n) 40 print n;"is ";: if not m then print "not "; 50 print "prime" 60 print "any key to continue" 70 poke 198,0:wait198,1:poke198,0 80 goto 20 -
Writing correct code is such a hassle, yet it has to be done to be able to run it, preferably without error in code, nor confusion in user.
-
Getting the formatting in a source code list right takes a lot of time and effort, if you’re doing it by hand. I guess I should just write about writing source code instead of showing it. Yeah, I know, the common saying is “show, don’t tell”, but showing is exhausting. Maybe I need a GitHub account.
-
Getting a foothold into 6502 machine language, part 4
Yeah, I know, I know. I promised a completed function to test if a number is prime. However, I want to write an article a day, and there’s only so much one can code in a day. This time I used code by other programmers, because, you know, I’m a novice. I did, however, try to understand the code, so I could rewrite where it was needed.
[ part 1 | part 2 | part 3 | part 5 | bonus ]
As established in part 3, we need two functions, one to square a number and one to take the modulo between two numbers. These will be the subjects of today’s article. I will analyze the original code, rewrite it, and test it with a Basic program, containing a machine code loader in data statements.
Here we go!
Binary division and the binary square
Suppose we wanted a 16-bit unsigned number to be divided by a non-zero 8-bit number to obtain its quotient and remainder. We are particularly interested in the remainder, since it’s the result of the modulo operation
dividend mod divisor, and we need it for checking divisibility (true if the remainder of a division is zero, otherwise false).On the website LLX.com about the Apple II, I found an article called Multiplying and Dividing on the 6502, written by Neil Parker. In the section “Dividing Arbitrary Numbers” it gets interesting for our purposes (modulo).
We will shift the bits of the dividend, one at a time, into a work area, and then try subtracting the divisor from the work area. If the subtraction succeeded, we replace the work area with the result of the subtraction and record a 1 bit in the quotient. If the subtraction failed, we discard its result and record a 0 bit in the quotient. The process is repeated until all bits of the dividend are used up.
Here are the steps:
- clear the remainder
- set the bit counter to 16
- shift the dividend to the left into the remainder
- trial subtract the divisor from the remainder
- was there a borrow (negative result), then step 8
- store the result in remainder
- increment the dividend (quotient)
- decrement bit counter
- if bit counter not zero, then step 3
There are three 16-bit registers, remainder, dividend and divisor. After exiting the routine, the dividend has become the quotient.
LDA #0 ;Initialize REM to 0 STA REM STA REM+1 LDX #16 ;There are 16 bits in NUM1 L1 ASL NUM1 ;Shift hi bit of NUM1 into REM ROL NUM1+1 ;(vacating the lo bit, which will be used for the quotient) ROL REM ROL REM+1 LDA REM SEC ;Trial subtraction SBC NUM2 TAY LDA REM+1 SBC NUM2+1 BCC L2 ;Did subtraction succeed? STA REM+1 ;If yes, save it STY REM INC NUM1 ;and record a 1 in the quotient L2 DEX BNE L1Since we aren’t interested in the quotient, just the remainder, we can eliminate the
INC NUM1the listing above. The divisor is smaller than 256, so an 8-bit version will do. We still need to go through 16 bits, though. We can setNUM2+1in Neil’s listing above to zero, by replacingSBC NUM2+1withSBC #$00.Here’s the new routine, I call “modulo”. For testing it in basic with a
SYScommand, I’ll use the freely available zero page addresses $FA through $FE to store the values. We start by POKEing the dividend in locations 250 and 251 (lo/hi bytes) and the divisor in location 252. The result will be in locations 253 and 254 (lo/hi bytes).; modulo.asm ; Calculate the modulo of an 8-bit number with a 16-bit number. ; Destroys all registers. num1 = $fa ; 16-bit dividend num2 = $fc ; 8-bit divisor rem = $fd ; 16-bit remainder *=$c000 ; can be called from Basic with SYS 49152 modulo: lda #$00 ; clear remainder sta rem sta rem+1 ldx #16 ; do 16 bits modloop: asl num1 ; shift num1 to the left rol num1+1 rol rem ; into remainder rol rem+1 sec lda rem ; do trial subtraction sbc num2 ; with divisor tay lda rem+1 sbc #$00 ; divisor is 8-bit value bcc modskip ; was there a borrow, then next bit sta rem+1 ; save the result sty rem modskip: dex ; repeat for 16 bits bne modloop rtsHere’s my test program, called “testmod 0.1”. It contains the converted hexdump from the Virtual 6502 Assembler after pasting in the above source listing “modulo.asm”.
10 rem testmod 0.1 20 forn=49152to49187:readb:poken,b:next:rem read in machine code 30 data 169,000,133,253,133,254,162,016 31 data 006,250,038,251,038,253,038,254 32 data 165,253,056,229,252,168,165,254 33 data 233,000,144,004,133,254,132,253 34 data 202,208,229,096 40 input "dividend";dd 50 input "divisor";dv 60 poke 251, int(dd/256):poke 250,dd-256*peek(251): rem poke dividend to memory 70 poke 252,dv:rem poke divisor to memory 80 sys 49152 90 rm=peek(253)+256*peek(254) 100 print "remainder is";rm 110 print "press any key to repeat" 120 poke 198,0:wait 198,1:poke 198,0:goto 40Here is some input and output I created in the C64 Basic interpreter of the V.I.C.E. C64 emulator on my Raspberry Pi-400, running Raspberry Pi OS.
run dividend? 61 divisor? 3 remainder is 1 press any key to repeat dividend? 65535 divisor? 16 remainder is 15 press any key to repeat dividend? 17 divisor? 4 remainder is 1 press any key to repeat break in 120 ready.It seems to work, nice job, me 😊
The same article on the site LLX.com mentions how to do multiplication, but what we need is a square function (a number multiplied by itself). So I found another resource on 6502.org, called Square Calculator and was written by by Lee Davison. It deals with signed integers, but we only need unsigned 8-bit integers, so there’s probably some rewriting to do, simplifying the code.
Here’s the full listing.
; Calculates the 16 bit unsigned integer square of the signed 16 bit integer in ; Numberl/Numberh. The result is always in the range 0 to 65025 and is held in ; Squarel/Squareh ; ; The maximum input range is only +/-255 and no checking is done to ensure that ; this is so. ; ; This routine is useful if you are trying to draw circles as for any circle ; ; x^2+y^2=r^2 where x and y are the co-ordinates of any point on the circle and ; r is the circle radius ; ; Destroys all registers *= 8000 ; these must be in RAM Numberl ; number to square low byte Numberh = Numberl+1 ; number to square high byte .word $FFFF Squarel ; square low byte Squareh = Squarel+1 ; square high byte .word $FFFF Tempsq: ; temp byte for intermediate result .byte $00 *= 8192 ; any address will do Square: LDA #$00 ; clear A STA Squarel ; clear square low byte ; (no need to clear the high byte, it gets ; shifted out) LDA Numberl ; get number low byte LDX Numberh ; get number high byte BPL NoNneg ; if +ve don't negate it ; else do a two's complement EOR #$FF ; invert SEC ; +1 ADC #$00 ; and add it NoNneg: STA Tempsq ; save ABS(number) LDX #$08 ; set bit count Nextr2bit: ASL Squarel ; low byte *2 ROL Squareh ; high byte *2+carry from low ASL A ; shift number byte BCC NoSqadd ; don't do add if C = 0 TAY ; save A CLC ; clear carry for add LDA Tempsq ; get number ADC Squarel ; add number^2 low byte STA Squarel ; save number^2 low byte LDA #$00 ; clear A ADC Squareh ; add number^2 high byte STA Squareh ; save number^2 high byte TYA ; get A back NoSqadd: DEX ; decrement bit count BNE Nextr2bit ; go do next bit RTSI like the coding practices of this author. The source code is easy to read and to the point.
After modifying Lee’s excellent source code listing, I came up with this listing, called “square.asm”. It squares an 8-bit unsigned integer into a 16-bit unsigned integer. Since I wanted to test it in Basic, I used the zero page addresses $FA through $FD, that are unused by the OS.
; square.asm ; ; Calculates the 16-bit unsigned square of an 8-bit unsigned integer. ; Destroys all registers. number = $fa ; 8-bit number to be squared squarel = $fb ; 16-bit squared number squareh = squarel+1 tempsq = $fd ; temporary storage of original number *=$c000 ; can be called from Basic with SYS 49152 square: lda #$00 ; clear A sta squarel ; clear square low byte ; (no need to clear the high byte, ; it gets shifted out) lda number ; get number in .A sta tempsq ; save original for later use ldx #$08 ; 8 bits to process sqloop: asl squarel ; shift square to left rol squareh ; (i.e. multiply by 2) asl a ; get next highest bit of number bcc sqnoadd ; don't do add if carry is zero tay ; save .A for later use clc lda tempsq ; add original number value adc squarel ; to square sta squarel lda #$00 ; add a possible carry adc squareh ; to the high byte of square sta squareh tya ; get .A back sqnoadd: dex ; decrement bit counter bne sqloop ; go do next bit rtsAgain, I assembled the assembly listing into a hexdump, pasting it into the source code field of the Virtual 6502 Assembler. I converted the hexdump into data statements for the following Basic program, called “tsquare 0.1”.
0 rem tsquare 0.1 10 forn=49152to49187:readb:poken,b:next:rem read in machine code 20 data 169,000,133,251,165,250,133,253 21 data 162,008,006,251,038,252,010,144 22 data 015,168,024,165,253,101,251,133 23 data 251,169,000,101,252,133,252,152 24 data 202,208,231,096 30 input "number";n 40 poke 250,n 50 sys 49152 60 s = peek(251)+256*peek(252) 70 print "square is";s 80 print "press any key to repeat" 90 poke 198,0:wait 198,1:poke 198,0:goto 30Here’s some values I tried:
run number? 2 square is 4 press any key to repeat number? 5 square is 25 press any key to repeat number? 49 square is 2401 press any key to repeat number? 255 square is 65025 press any key to repeat number? 0 square is 0 press any key to repeat break in 90 ready.I love when code works at first attempt. Of course, I had lots of help from people from the past. Still, it’s satisfying if things work as they should.
-
Reading through 6502 assembly code listings for my current article on assembly programming on the C64, I can see there’s an art to writing clear and easy-to-read code. Some are better at it than others. I suppose I should “steal” some of those practices (read: make them my own).
-
Getting a foothold into 6502 machine language, part 3
This should get more interesting than the previous two parts. We want a
usrfunction that tests if a number between 0 and 65535, inclusive, is a prime number. We expect an a result of thisusrfunction either a-1(true) or a0(false). I really should split this whole thing into four parts to keep it somewhat manageable (for those who follow along):- thinking about the problem
- formulating a rough algorithm in words
- formulating an assembly language routine
- testing an confirming if the code is correct
[ part 1 | part 2 | part 4 | part 5 | bonus ]
As for the assembly language routine, I will limit myself in this part to a generator of possible prime numbers. I can use this generator to test primality of a number that was input through the
usrfunction in Basic. But since I wanted to finish this article in a day, the completed function will have to wait until part 4.Coding correctly takes time, after all.
Some logical reasoning about a prime number sieve algorithm
Using the article on Geeks for Geeks on prime numbers, I did some simple logical reasoning to determine an algorithm to find out whether or not a number is prime. We can easily generate prime numbers between 2 and 43, inclusive. This means we can quickly test a number’s primality up to the value 1850. After that, we need to use the formula
6 * n ± 1for values ofnlarger than 7 thereafter, though not all of those are primes.- a prime number is a whole number larger than one that is only divisible by one and itself.
- the number 2 is the only even prime number
- the number 3 is the lowest odd prime number
- the number 5 is the one but lowest odd prime number
- the number 7 is the two but lowest odd prime number, and also the lowest consecutive odd number larger than 1 that is prime
- any odd number not divisible by either 2, nor 3 is a candidate prime number, meaning any candidate prime number larger than 3 is of the formula:
…6 * n - 1, or
…6 * n + 1,
… withnequal to a whole positive number
… after having tested for the values 2, 3, 5, and 7,nmust be a whole number larger than one - a non-prime is the product of two primes, and the largest possible product of two primes that is equal to a non-prime is the square of a prime, in other words, if a number isn’t divisible by prime numbers that are less than or equal to the square root of that number, that number is prime, in yet other words:
… when testing a number for divisibility by primes, then highest possible prime number to test for is:
…p <= sqrt(n), where
…pis a prime number andnis the number to be tested for primality - since 7 is the lowest consecutive odd prime, we can determine the highest value of
nthat gives a number that is always prime, never a non-prime
…(6 * n - 1 < 7 * 7)or(6 * n + 1 < 7 * 7),
…(n < (7 * 7 + 1) / 6)or(n < (7 * 7 - 1) / 6)
…n < 8 - summarizing (some of) the above, primes between 2 and 43 can be determined by being equal to:
…2, 3, 5, 7
… or calculated as:
…6 * n - 1,6 * n + 1for1 < n < 8
… the lowest non-prime that can’t be easily determined by using these primes is an odd number larger than the square of 43, which is 1851.
An algorithm for testing primality
So, up to a value of 1850 we can generate primes to test if a number is prime. For higher numbers we can only generate possible primes, though that isn’t a problem, since if a number is divisible by a product of primes, it isn’t prime either. It would be nice, though, to have a method to eliminate some of the non-primes to test with. The article on Geeks for Geeks mentions some additional methods to do just that. However, let us first use what is somewhat easy to understand, without a degree in mathematics.
As a first approach, using the
6 * n ± 1formula to generate primes to test with is a solid method. We need a “next prime” function, where the input valuekdetermines the k-th prime, withk >= 0. For primes up to 43 we can simply test if a number is equal to the output of this function, since every output number is a prime. However, we only have to test for primes which square values are smaller than the number that is being tested.- clear primality flag (assume it’s not a prime)
- endless loop
- fetch next prime
- if
number < prime * primethen exit loop - if
number == primethen set primality flag, exit loop
- return primality flag
If a prime number from the prime number generator function becomes larger than 43, we must stop testing for equality (since the value that is output isn’t necessarily prime), and start testing for divisibility instead. We want it to be tested as follows:
- set primality flag (assume it’s a prime)
- endless loop
- fetch next prime
- if
number < prime * primethen exit loop - if
number mod prime == 0then it’s no prime, exit loop
- return primality flag
To distinguish between the two:
- if
number <= 43then compare with primes, else test with “primes”
Putting it all together
Time to fetch the code editor and start mashing keys.
Let’s first test our prime number generator. It has to output a whole positive number based on a whole non-negative number input. However, remember that we only have a function in ROM to output a signed integer, so we have to convert our unsigned integer to a signed one, and convert it back to an unsigned integer in Basic, by subtracting and adding 32768, respectively.
*= $c000 ; usrfunction 0.3 ; generate a candidate prime number, ; based on the 16-bit unsigned integer input, ; representing the order of the prime ; output the prime number as a signed 16-bit integer ; to work around the limitation of the Basic ROM ; (there's no function to convert a unsigned integer ; into a real number) ; in basic, add 32768 to the output of the usr function ; for example (ignoring that the output is signed) ; prime(0) = 2 ; prime(1) = 3 ; prime(2) = 5 ; etc. getadr = $b7f7 givayf = $b391 fac1int = $64 fac2int = $66 jsr getadr ;convert real into unsigned int in .A and .Y (hi/lo) jsr prime ;generate the nth prime sec sbc #%10000000 ;subtract $8000 (32678) to make it a signed integer jmp givayf ;make it real and return to Basic prime: ;generate the nth prime number ;input .A and .Y as hi/lo byte of 16-bit unsigned integer ; indicating the order of the prime ;output .A and .Y as hi/lo byte of 16-bit unsigned integer ; containing the nth prime number on the number line ;e.g. prime(0) -> 2, prime(1) -> 3, prime(2) -> 5, etc. ;only numbers generated up to 43 are guaranteed prime, ; larger numbers may be prime, ; or co-prime (product of 2 or more primes) cmp #0 bne prime2 ;order is too big, skip 0 and 1 cpy #0 ;order == 0? bne prime1 ;no, check for 1 ldy #2 ;prime(0) = 2 rts prime1: cpy #1 ;order == 1? bne prime2 ;no, check for 2 and up ldy #3 ;prime(1) = 3 rts prime2: ;calculate primes for (order > 1) ;in the formula (6 * n ± 1), where n is equal to (order / 2), lsr ;n = (order / 2) sta fac1int tya ror sta fac1int+1 asl fac1int+1 ;k = n * 2 rol fac1int lda fac1int ;m = n * 2 ldx fac1int+1 sta fac2int stx fac2int+1 asl fac2int+1 ;m = n * 4 rol fac2int clc ;add m to k, to get (6 * n) lda fac1int+1 adc fac2int+1 sta fac1int+1 lda fac1int adc fac2int sta fac1int tya ;retrieve original lo byte of order and #1 ;is it odd? cmp #1 beq prime3 ;then add 1 to (6 * n) sec ;else subtract 1 from (6 * n) lda fac1int+1 sbc #1 tay ;lo byte of ((6 * n) - 1) in .Y lda fac1int sbc #0 ;hi byte of ((6 * n) - 1) in .A rts prime3: clc ;add 1 to (6 * n) lda fac1int+1 adc #1 tay ;lo byte of ((6 * n) + 1) in .Y lda fac1int adc #0 ;hi byte of ((6 * n) + 1) in .A rtsGive our code a spin, testing its validity
I pasted the source code into Virtual 6502 Assembler, copied the hexdump, and converted with a calculator app into decimal values of data statements in the Basic program “testusrf 0.3” below.
0 rem testusrf 0.3 10 poke 785,0:poke 786,192:rem set usr address to $c000 20 forn=49152to49246:readb:poken,b:next:rem read in machine code 30 data 032,247,183,032,012,192,056,233 31 data 128,076,145,179,201,000,208,014 32 data 192,000,208,003,160,002,096,192 33 data 001,208,003,160,003,096,074,133 34 data 100,152,106,133,101,006,101,038 35 data 100,165,100,166,101,133,102,134 36 data 103,006,103,038,102,024,165,101 37 data 101,103,133,101,165,100,101,102 38 data 133,100,152,041,001,201,001,240 39 data 011,056,165,101,233,001,168,165 40 data 100,233,000,096,024,165,101,105 41 data 001,168,165,100,105,000,096 50 for x = 0 to 9:gosub 100:next 99 end 100 print "x =";x;", usr(x) =";usr(x)+32768:returnRunning this program for the first 100 “primes” gave this output:
list 50 50 for x=00000 to 00099:gosub 100:next ready. run 2 3 5 7 11 13 17 19 23 25 29 31 35 37 41 43 47 49 53 55 59 61 65 67 71 73 77 79 83 85 89 91 95 97 101 103 107 109 113 11 5 119 121 125 127 131 133 137 13 9 143 145 149 151 155 157 161 16 3 167 169 173 175 179 181 185 18 7 191 193 197 199 203 205 209 21 1 215 217 221 223 227 229 233 23 5 239 241 245 247 251 253 257 25 9 263 265 269 271 275 277 281 28 3 287 289 293 295 ready.I noticed this:
print usr(21845)+32768,usr(21846)+32768 65533 1 ready.This is because the prime number generator doesn’t check for any value overflow. The value
1is actually the value65537, but the 17th bit of the latter number doesn’t exist, so the value wraps around to1.print (65533 - 1)/6 10922 ready.So the prime function gives valid answers up to the 10922th prime, which is more than enough to test if the largest 16-bit unsigned value (65535) is prime. For that we need at most a prime of the square root of that value, which is slightly less than 256. These “primes” are already visible in the first 100 “primes”.
Did I do it right?
To check, you can compare the output of the prime number generator with the List of Prime Numbers on Wikipedia. We are only concerned with primes less than 256, since it’s the square root of the value 65536. 65536 is already higher than the maximal value of a 16-bit unsigned integer number (65535). To speed things up, we could’ve just as well hard-coded the list of 54 primes that are less than 256. The routine would need more bytes, though.
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251The prime numbers from the Wikipedia page are all included in the output of “testusrf 0.3” in the listing above. The prime generator does output some extra (non-prime) numbers, that don’t do any harm when testing for primality.
-
Getting a foothold into 6502 machine language, part 2
I mentioned in part 1 that there’s a convenient routine to convert a real number into a signed 16-bit integer. However, Basic line numbers are 16-bit unsigned numbers when parsed into Basic code. So there has to be a routine to turn a real value in fac1 into a 16-bit integer as part of the interpretation of Basic text that starts with a line number.
[ part 1 | part 3 | part 4 | part 5 | bonus ]
And indeed there is. It is called getadr and is located at $b7f7. It supposedly is to turn a real value between zero and 65536 into a 16-bit unsigned integer. For both values the floating point accumulator fac1 is used. The resulting integer value is stored in locations $64 and $65 of fac1, high byte first.
Since the
usrmachine language routine stores the function value entered in Basic into fac1 as a real number, the next steps should be easy:- call getadr ($b7f7) to convert a real into a unsigned 16-bit integer
- read $64 in .A and $65 in .Y, both part of fac1
- process the integer into a value stored in .A and .Y
- subtract 32768 to convert the unsigned integer into a signed integer value between -32768 and 32767, which givayf needs
- turn .A and .Y into a real, by calling the givayf ($b391) routine
To not over-complicate things at this point, we should interpret the “process the integer” as “do nothing”, effectively skipping the processing step. We will develop our “is this number prime” routine later. All we want to know if the supplied value between 0 and 65536 is accepted and can be used as such.
This method is certainly somewhat error-prone (never underestimate the power of typos), because it requires some workaround in Basic to deal with the signed integer value that our
usrmachine language routine returns to Basic.After entering the source code in the assembly listing “usrfunction 0.2”, I copied the hexdump from Virtual 6502 Assembler and wrote the Basic program “testusrf 0.2” in the next listing to see if I got it right. This was what I wanted to test:
- boundaries 0 and 65535
- fractional numbers between 0 and 65536, exclusive—use a few values of the expression
65536*rnd(ti) - errors with numbers that are < 0 or >= 65536 (use -1 and 65536)
*= $c000 ; usrfunction 0.2 ; use an unsigned integer ; and, for now, do nothing with it getadr = $b7f7 givayf = $b391 fac1int = $64 jsr getadr ;convert real into unsigned int lda fac1int ;load high byte in .A ldy fac1int+1 ;load low byte in .Y nop ;do nothing for now sec sbc #%10000000 ;subtract $8000 (32678) to make it a signed integer jmp givayf ;make it real and return to Basic0 rem testusrf 0.2 10 poke 785,0:poke 786,192:rem set usr address to $c000 20 forn=49152to49165:readb:poken,b:next:rem read in machine code 30 data 32,247,183,165,100,164,101,234 40 data 56,233,128,76,145,179 70 x=0:gosub 100 80 x=65535:gosub 100 90 for i=0 to 9:x=rnd(ti)*65536:gosub 100:next 99 end 100 print "x =";x;", usr(x) =";usr(x)+32768:returnHere is the output of that Basic program, with two values entered by hand, which should throw error messages:
run x = 0 , usr(x) = 0 x = 65535 , usr(x) = 65535 x = 12161.1233 , usr(x) = 12161 x = 3073.54893 , usr(x) = 3073 x = 54247.0177 , usr(x) = 54247 x = 36356.0453 , usr(x) = 36356 x = 58801.1164 , usr(x) = 58801 x = 37546.6392 , usr(x) = 37546 x = 54977.7024 , usr(x) = 54977 x = 61029.0648 , usr(x) = 61029 x = 12345.8034 , usr(x) = 12345 x = 63762.592 , usr(x) = 63762 ready. ?usr(-1) ?illegal quantity error ready. ?usr(65536) ?illegal quantity error ready.It worked, which is always a relief.
Now the routine we want (“is this number prime?") doesn’t have to result into an unsigned 16-bit value. We only want to be able to input such a value. The output we expect is either a “Yes” (-1) or “No” (0). So a signed 16-bit integer is exactly what we need.
So why did I do this workaround? I wanted to know if it is at all possible to work around this limitation, in case I ever needed that. It certainly is, as the Basic example shows.
In part 3 I will (finally) start coding for the question whether or not the supplied number is a prime number. This should be interesting.
-
Getting a foothold into 6502 machine language, part 1
It seems in Commodore Basic version 2 the preferred way to get a value into a user-defined 6502 machine language routine (and to get a value back), is the
usrfunction. It took me some trial and error to get it to work. Luckily, Google is Your Friend, or, in my case DuckDuckGo. I also used “Mapping the Commodore 64”, by Sheldon Leemon, which can be downloaded as PDF on Archive.org. If you’re serious about 6502 assembly language on the Commodore 64, I highly recommend this book.[ part 2 | part 3 | part 4 | part 5 | bonus ]
First of all, how do we get the
usrfunction to work? Simply runningprint usr(42)results in an error message.Apparently, one has to set the address of the start of one’s own machine language routine. After (re)booting the operating system the value is set to $b248 (fcerr routine, which prints an
illegal quantityerror). Taking a step back, the final step of the routine in Basic ROM that interprets theusrfunction is jumping to address $0310 in RAM:0310 4c 48 b2 jmp $b248So all one has to do is overwrite the address of this
jmpinstruction so it points to the user defined machine language routine. This address is located at $311 and $312, in the usual low byte high byte order of the 6502 machine language. If the user defined routine is, for example, located at $c000 (49152), the values $00 and $c0 have to be written in $311 and $312, respectively.In Basic we use decimal instead of hexadecimal:
- $311 is 785 decimal
- $312 is 786 decimal
- $c0 is 192 decimal
10 poke 785,0:poke 786,192We always have to keep in mind that Commodore Basic uses real values, never integers. The value we supplied to the
usrfunction in our Basic code is stored into fac1, which consists of six bytes, starting at location $61. Luckily, this isn’t all that important here, since there are two handy functions to convert real values back and forth into 16-bit signed integer values, using fac1. They are:- $b1aa – Convert a Floating Point Number to a Signed Integer in .A and .Y Registers, which calls the ayint routine (located at $b1bf), and loads the resulting signed 16-bit integer value into registers .Y and .A (lo/hi).
- $b391 – givayf Convert 16-Bit Signed Integer in registers .Y and .A (lo/hi) to a Floating Point Number
In both instances the registers .Y and .A contain the low byte, and high byte of the 16-bit signed integer, respectively.
But, wait, what is a “16-bit signed integer” exactly? Well, in the 6502 architecture, this is the 2’s-complement representation of a whole number between -32768 and 32767, inclusive. It simplifies addition and subtraction of whole numbers, either positive, negative, or zero. If you want to know more, read the relevant Wikipedia article.
The thing is that if you pass a zero or a positive value into the
usrfunction and convert it into an integer in your machine language routine, it has to be between 0 and 32767, inclusive. If your machine code routine can deal with that restriction, you’re okay. Of course, you could use the real value instead, or use some trickery to use integers between 0 and 65535, inclusive. Whatever the routine does exactly is up to you, since you are defining it.Perhaps I should give an example of how to use the
usrfunction in a useful manner 😉What if I wanted to know if a value I put into the
usrfunction is a prime number, divisible only by itself or one, but no other whole positive number? That is a tricky problem to solve, since the 6502 has no division, nor multiplication instructions built in (it has to be done in software instead, using a set of instructions). Other than that, finding out a whole number is prime isn’t straightforward either, at least, if you want the method to be efficient and correct.To not reinvent the wheel, I looked for someone who had done the work before, and found Geeks For Geeks - Prime Numbers as a resource. Let’s go with that!
Anyway, the result of our
usrfunction should be either true or false, which is in Commodore Basic represented by a-1and0, respectively:print 1=1,1=0 -1 0 ready.To understand all this, I used a minimal viable solution. My code should test if the value put into the
usrfunction and converted into a signed integer is even. If so, it should return a-1, else a0. We still need to convert the result of parity test into a real number before exiting our routine in 6502 assembly language.*= $c000 ; usrfunction 0.1 ; test if the usr function even works ; as a test, check for even parity getayf = $b1aa givayf = $b391 jsr getayf tya ;lo byte and #%00000001 ;mask out every bit except bit 0 cmp #0 beq iseven lda #$00 ;false, which is 0 in 16-bit signed integer tay ;corresponding to the hex value $0000 jmp givayf ;make it real, return to Basic iseven: lda #$ff ;true, which is -1 in 16-bit signed integer tay ;corresponding to the hex value $ffff jmp givayf ;make it real, return to BasicI wrote this routine in the Textastic app on my iPad, used the Virtual 6502 assembler to create a hex dump, used it to create the Basic program below, typed that into the V.I.C.E. C64 emulator on my Raspberry PI-400 running Raspberry Pi OS, and ran it.
10 poke 785,0:poke 786,192: rem set usr address to $c000 (49152) 20 forn=49152to49173:readb:poken,b:next:rem read in machine code 30 x=int(rnd(ti)*100):rem random number between 0 and 99, inclusive 40 print x;" is "; 50 if usr(x) then print "even":goto 70 60 print "odd" 70 data 32,170,177,152,41,1,201,0,240,6 80 data 169,0,168,76,145,179,169,255,168,76,145,179It worked. Pfew!
Now we can tackle more complicated matters, but that has to wait until part 2, because this article is already much longer than I anticipated, and I started to make mistakes. I need a break.
-
Currently reading: Mapping the Commodore 64 by Sheldon Leemon 📚
Why would you even want to use the C64, it’s an old computer? It isn’t old, it’s retro!
