-
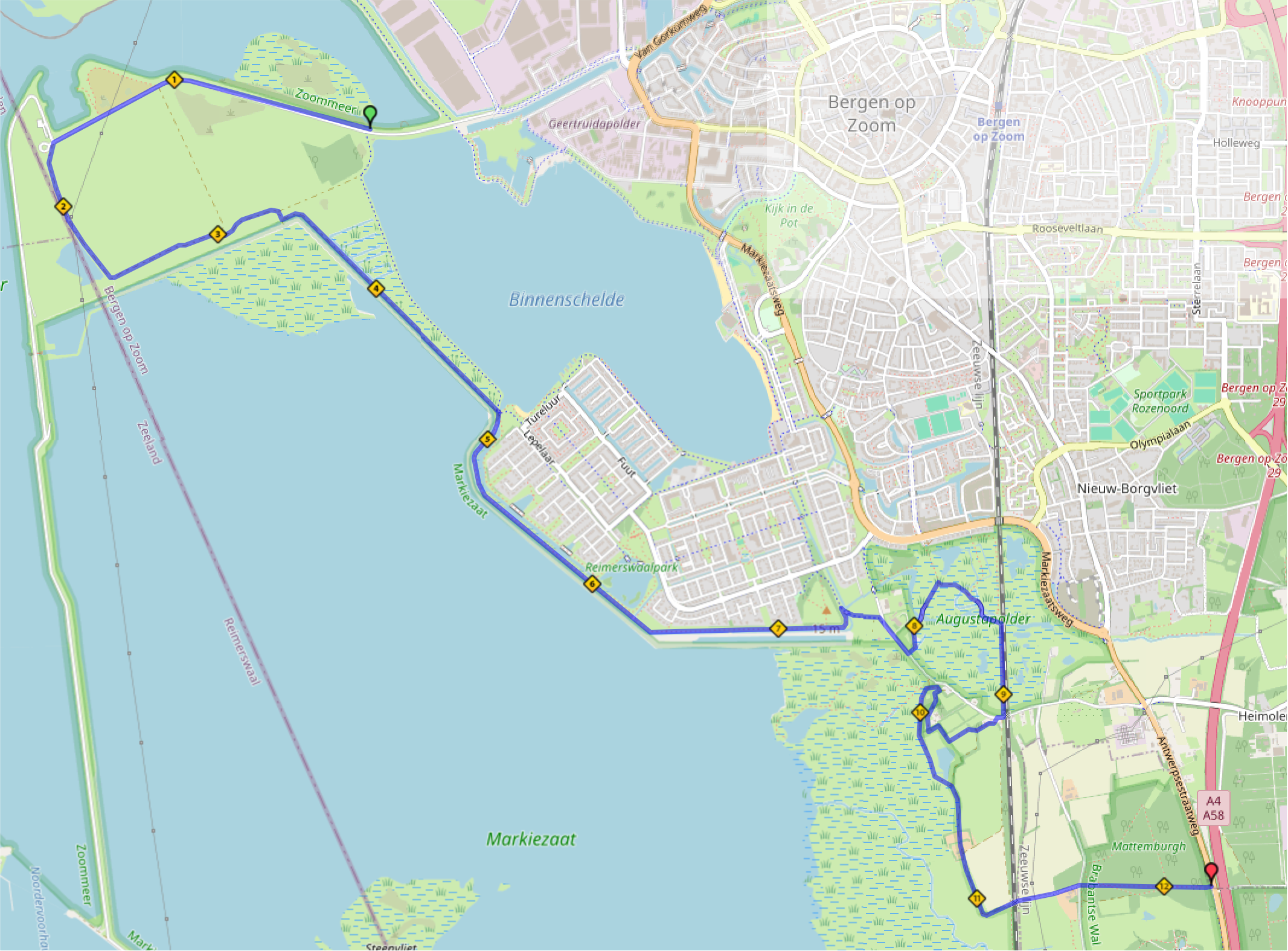
To get accustomed to some rough terrain in my half marathon race in September, I’ll run my 73 minutes run at base tempo on similar oneven footpaths coming Wednesday (see map). It won’t be as brutal as the Kustloop, but I suppose it’s a better preparation than only training on asphalt.
-
It looks like my race next Sunday will be canceled due to high temperatures. I asked to the organizers if runners could run on their own and get credit for it, as in run your own race during the COVID-19 pandemic. I don’t expect a response, but I had to try. I can see the potential problems.
-
It had been six months since I ran a sub-2 hours half marathon (and got a hip injury from over-training). I got a modest 485th place out of 739 runners. The goal for 2025 is a sub-4 hours marathon.

-
I now have to take off my Garmin watch before I start drawing art, because when I come into a flow, the watch registers it as “asleep.” It messed up my training readiness, since a three hours sleep period is deemed “too short and detrimental.” That is computers judging personal health for you.
-
While it’s fun to run races, it’s the training to prepare for those race which takes up most of the time. It also takes a lot of time to make one’s own training schedule that is balanced, tough enough to improve (or maintain) one’s fitness, yet flexible enough to appear recovered at the race.

-
I’m happy I ditched Strava in time, with their AI cr!$p. Now they’ve bought Runna as well, another AI-powered service. I’m sure free users will be bombarded with “promotions” to join Strava, because, guess what, the customers have to pay for all of that. The general consensus is Strava’s AI is bad.
-
I finished my marathon in Rotterdam, The Netherlands. Despite the worst preparation in years, I beat the time Runalyze predicted by more than 3 minuten. My official nett time was 4h42m48s (6:43 min/km, 10:48 min/mi). Especially after the 32 K mark it became exceedingly hard to keep running.

-
Today I ran a half marathon race to determine my marathon goal five weeks from now. With 2h06m16s I could go for a 4h15m marathon, yet 4h30m seems a safer bet, especially because I was heavily injured for four month, in which I could hardly train, or only very slowly.

-
Checking out specific details on the Marathon Rotterdam website, since it’s only five weeks and one day before I’ll be running my fifth marathon. No, the details aren’t there yet, so I’ll have to be patient. Probably will receive an email about those anyway.
-
I ran my first long endurance run, seven weeks before I want to run the Rotterdam Marathon (April 13). As expected, today wasn’t easy, but I’m confident I will cross the finish line. The injury that was plaguing me since October 2024 seems to have cured itself, by reducing mileage and speed. Yay me!
-
It seems I’m on my way back from a hip injury. I may even run the Rotterdam Marathon this year, though with readjusted expectations. I couldn’t put in the hours and am seriously overweight now. Still, it’s nice to enjoy life again without constant pain. Against expectations, it made time fly.
-
Apparently, in 2024 out of the 70,000 inhabitants of my hometown, only 56 people (8 in 10,000) started in the Marathon Rotterdam. Nationwide that’s 17,000 marathon runners out of 18,000,000 people (9 in 10,000). While running is on the rise since COVID19, the marathon is still a niche distance.
-
Despite an injury I developed after my half marathon race two weeks ago, I’m going to run a marathon next Sunday. I already know what went wrong (lack of specific strength), and how to prevent it next time—I need to do the supplementary exercises I used to do, like hops and jumps, and running up a stair, several steps at a time, besides the usual exercises like crunches, planks, lunges and push-ups.
So, in order to not stress my body too much, I lowered my expectations for the upcoming marathon race, by starting at a 4:30 hours pace (6:20 min/km, 10:11 min/mi), and perhaps speeding up after the 35 km mark. It’s a sound strategy, provided the injury is cured (enough). I replaced running by bicycling a week ago.
I suppose I’m (re)learning by making mistakes. I really can’t fault myself, because the trainer I’m paying my track & field club for has never materialized. There’s someone, but he’s only interested in faster runners at shorter distances (3 to 10 km). Maybe I should hire a coach, though that’s rather costly, even an online coach or an app like Runna. Doing it all yourself is unnecessarily hard.
🏃♂️👈42.2 km👉🏃♂️➡️
-
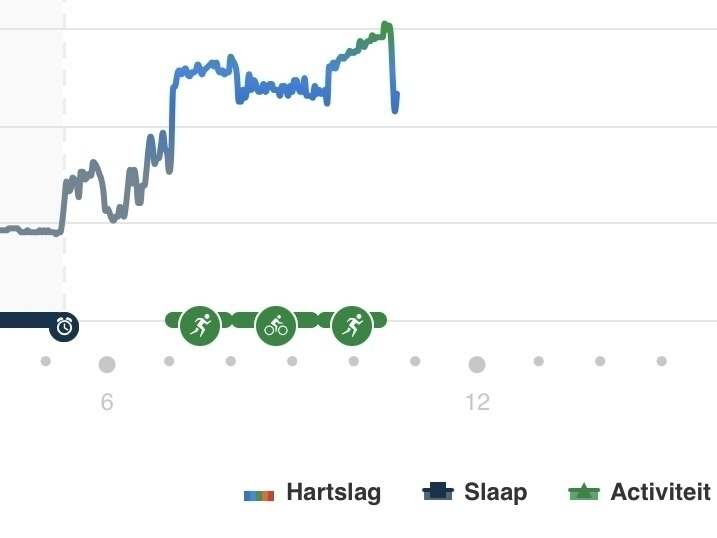
Yesterday I noticed pain in my achilles tendon, so I decided to replace some running by cycling. I recorded using a triathlon app on my watch. Two things went wrong. I accidentally wiped the activity, but, worse, I underestimated the bike ride and the heat. It was too long and too fast. 🏃♂️🚴♂️
-
I’m looking for inspiration by following marathon runners on Strava. Got discouraged by a member of my T&F club, who claimed she could run a marathon on 27 km per week as a base, because she wasn’t able to put in the time. Alas, she’s not the only member who lost respect for the marathon.
🏃 -
Last Saturday I did a 30 km training run as a (300 m run, 100 m walk) run-walk-run in 3h38m, about 50% slower than my fastest ever 30 km race in 2016. Corrected for heart rate it’s only 25% slower, and for weight 10% slower. That difference could be largely explained by the walking. 🏃♂️
-
I find it interesting to predict one’s time in an important running race based on a test run, as to know what a good pace is to keep up during that race. I always used a self-conceived rule, which is quite different from the generally accepted rule according to research engineer Peter Riegel, although it took some math to figure that out (see below).
Self-conceived rule
I have experienced for myself early on in my running career that my pace increases by a factor of 1.07 when doubling the running distance, under ideal circumstances. For example, a 10 km race tended to be 7 percent slower than a 5 km race. I generalized this idea into a formula.
1: p2 ÷ p1 = 1.07 n
2: d2 ÷ d1 = 2 n
1 & 2 ⇒ n = ²log(d2 ÷ d1)
p2 ÷ p1 = 1.07 ²log(d2 ÷ d1)
p2 = p1 × 1.07 ²log(d2 ÷ d1)
p1 = t1 ÷ d1; p2 = t2 ÷ d2
⇒ t2 ÷ d2 = (t1 ÷ d1) × 1.07 ²log(d2 ÷ d1)
t2 = t1 × (d2 ÷ d1) x 1.07 ²log(d2 ÷ d1)
Factors for 1.07 ²log(d2 ÷ d1)
The table below shows some favorite distances from road races. In the rows are the distances from which the pace is known and in the columns the distances from which the corresponding factors can be read as numbers in the table. Multiplying a known pace for a particular distance with this factor gives the corresponding unknown pace for another distance. For example, for a 15 km race (third row in the table) multiply this race’s pace by a factor of 1.1062 to calculate the ideal pace for a marathon (eighth column in the table). A sub-3 hour marathon would require a sub-36 minutes 10 km, according to this table.
5 km 10 km 15 km 10 mi 20 km ½ mar 30 km mar 5 km 1.0000 1.0700 1.1132 1.1208 1.1449 1.1509 1.1911 1.2314 10 km 0.9346 1.0000 1.0404 1.0475 1.0700 1.0756 1.1132 1.1509 15 km 0.8983 0.9612 1.0000 1.0069 1.0285 1.0339 1.0700 1.1062 10 mi 0.8922 0.9546 0.9932 1.0000 1.0215 1.0268 1.0627 1.0987 20 km 0.8734 0.9346 0.9723 0.9790 1.0000 1.0052 1.0404 1.0756 ½ mar 0.8689 0.9297 0.9673 0.9739 0.9948 1.0000 1.0350 1.0700 30 km 0.8395 0.8983 0.9346 0.9351 0.9612 0.9662 1.0000 1.0339 mar 0.8121 0.8689 0.9040 0.9102 0.9298 0.9346 0.9673 1.0000 Rule according to Riegel
According to Peter Riegel the increase in pace for a longer distance is radically different:
t2 = t1 × (d2 ÷ d1) 1.06
For times between about 3 and 230 minutes.
t2 = t1 × d2 1.06 ÷ d1 1.06
t2 ÷ d2 = t1 × (d2 1.06 ÷ d2) ÷ d1 1.06
t2 ÷ d2 = t1 × d2 1.06 - 1 ÷ d1 1.06
t2 ÷ d2 = t1 × d2 0.06 ÷ (d1 × (d1 1.06 ÷ d1))
t2 ÷ d2 = t1 × d2 0.06 ÷ (d1 × (d1 1.06 - 1))
t2 ÷ d2 = (d2 0.06 ÷ d1 0.06) × (t1 ÷ d1)
t2 ÷ d2 = (d2 ÷ d1) 0.06 × (t1 ÷ d1)
p1 = t1 ÷ d1; p2 = t2 ÷ d2
⇒ p2 = (d2 ÷ d1) 0.06 × p1
If the distance doubles, the pace increases by a factor of 2 0.06, or 1.0425. That would mean that as the distance increases, the pace increases drastically less than with the aforementioned calculation method of my own.
A similar table is shown below, containing factors to be multiplied with known paces to calculate unknown paces, depending on the distances.
Factors for the Riegel calculation
The table below shows some favorite distances from road races. In the rows are the distances from which the pace is known and in the columns the distances from which the corresponding factors can be read as numbers in the table. Multiplying a known pace for a particular distance with this factor gives the corresponding unknown pace for another distance. For example, for a 15 km race (third row in the table) you can multiply the pace by a factor of 1.0640 to calculate the ideal pace on a marathon (eighth column in the table). For a sub-3 hour marathon, a time of sub-39 minutes on the 10 km is fast enough, according to this table.
5 km 10 km 15 km 10 mi 20 km ½ mar 30 km mar 5 km 1.0000 1.0425 1.0681 1.0726 1.0867 1.0902 1.1135 1.1365 10 km 0.9593 1.0000 1.0246 1.0289 1.0425 1.0458 1.0681 1.0902 15 km 0.9362 0.9760 1.0000 1.0042 1.0174 1.0207 1.0425 1.0640 10 mi 0.9323 0.9719 0.9958 1.0000 1.0131 1.0164 1.0381 1.0596 20 km 0.9202 0.9593 0.9829 0.9870 1.0000 1.0032 1.0246 1.0458 ½ mar 0.9172 0.9562 0.9797 0.9839 0.9968 1.0000 1.0213 1.0425 30 km 0.8981 0.9362 0.9593 0.9633 0.9760 0.9791 1.0000 1.0207 mar 0.8799 0.9172 0.9398 0.9438 0.9562 0.9593 0.9797 1.0000 What to use?
It seems rather obvious to me that a generally accepted rule makes more sense than something you came up with yourself based on your own race results. Other than that, there are strict limits to when the rule according to Riegel applies. For slow runners (e.g. marathon in 4½ hours) or extremely short distances (e.g. 400 m) the rule does not apply, or, at least, the prediction value will be rather low.
An acquaintance of mine ran a time of 1h01m36s in a “15 km” race (14.87 km according to his GPS). According to my calculation, that would be enough for 3h15m39s on a marathon with certified course (1% longer than 42.195 km). According to Riegel, it would be enough for 3h08m03s on the same certified marathon course. In both cases, the result of the “15 km” race was too slow for an “official marathon” (i.e. with certified course) under 3 hours. A sub-3 hour marathon would have required a time of 56m40s or 58m57s for the “15 km” race (my rule, Riegels rule respectively). This acquaintance has to get faster somehow, either by training and/or good fueling during the race. Ideal circumstances would help too.
Anyway, I think I can put my home-grown calculation method to rest and start using the much better tested method according to Peter Riegel.
-
In preparation for a half marathon on King’s Day (April 27) I ran and walked 24 km. I’m still suffering through an ankle injury, so I’ll have to be cautious. It was a beautiful day, partially run alongside a canal between two rivers. It was tough, because I did 1.5 times my usual training 🏃




-
Someone dug a trench across a footpath, and I stepped right into it, hurting my ankle badly. Who does such a thing, making a trap for pedestrians? The ankle is swollen and hurts, but not enough to go to a doctor. I suppose R.I.C.E. will reduce the swelling, as in Rest, Ice, Compression, Elevation.
-
If everything goes as planned, I will have run around 3300 km (2050 mi) in 2023 when the New Year rolls around. With a little over 5 weeks to go, I’ve already passed 2930 km of running this year, an average of 63 km (39 mi) weekly, 272 km (169 mi) monthly, despite injuries and other mishaps. 🏃♂️