-
I made a rough animation in the Animatic app on iPad and traced the frames into a pixel animation with Pixaki. It took much longer than I expected, but I’m pleased with the (very rough) result running on my Pixoo64 LED panel.

-
I can’t escape the thought that BlueSky verification is another nail in the coffin of anonymity, which can be legit. Those up to no good just use identity theft to get around this trend of spying on people.
-
Not sure why servicing the connection to the Internet by one’s provider requires an outage, but I did have one of those for somewhat less than an hour. It was announced, but I missed it. Still, why the required outage?
-
While it’s fun to run races, it’s the training to prepare for those race which takes up most of the time. It also takes a lot of time to make one’s own training schedule that is balanced, tough enough to improve (or maintain) one’s fitness, yet flexible enough to appear recovered at the race.

-
I’m happy I ditched Strava in time, with their AI cr!$p. Now they’ve bought Runna as well, another AI-powered service. I’m sure free users will be bombarded with “promotions” to join Strava, because, guess what, the customers have to pay for all of that. The general consensus is Strava’s AI is bad.
-
I finished my marathon in Rotterdam, The Netherlands. Despite the worst preparation in years, I beat the time Runalyze predicted by more than 3 minuten. My official nett time was 4h42m48s (6:43 min/km, 10:48 min/mi). Especially after the 32 K mark it became exceedingly hard to keep running.

-
About task lists. Once I’ve finished a task, I’m done with it. I keep forgetting I’ll have to update the list constantly. This hasn’t changed since iOS 7 and before. I get no kick out of checking off items, and find it a bore.
-
I’ll be running a marathon on 13 April 2025. It almost didn’t happen because of injuries, which only healed a week ago. To celebrate in advance I made this jumble of legs, arms, and a confused head. Its animation lives on the Divoom community, where I became a master pixel artist, also this week.

-
Using Quick Poses I found a reference for a pose. After pixeling the nude I put some clothes on her to avoid flagging on the Divoom community. BTW, it wasn’t quick at all.

-
A larger piece, and Fate/Apocrypha fan art. I know I can do better, if I weren’t so out of practice. I also might have traced a little to get it done, after spending more than 12 hours on it today,

-
It’s been a while since I posted some pixel art on here, while I’ve been inundating the Divoom community with my creations, being mostly recommended by the staff. I don’t judge it high art, but I can see why they want to see more of it. Most don’t seem to post anything, or at best it’s low-effort.

-
Seen on my 8 km long walk today. This obelisk commemorates 75 years of independence of the Kingdom of the Netherlands on 17 November 1813.

-
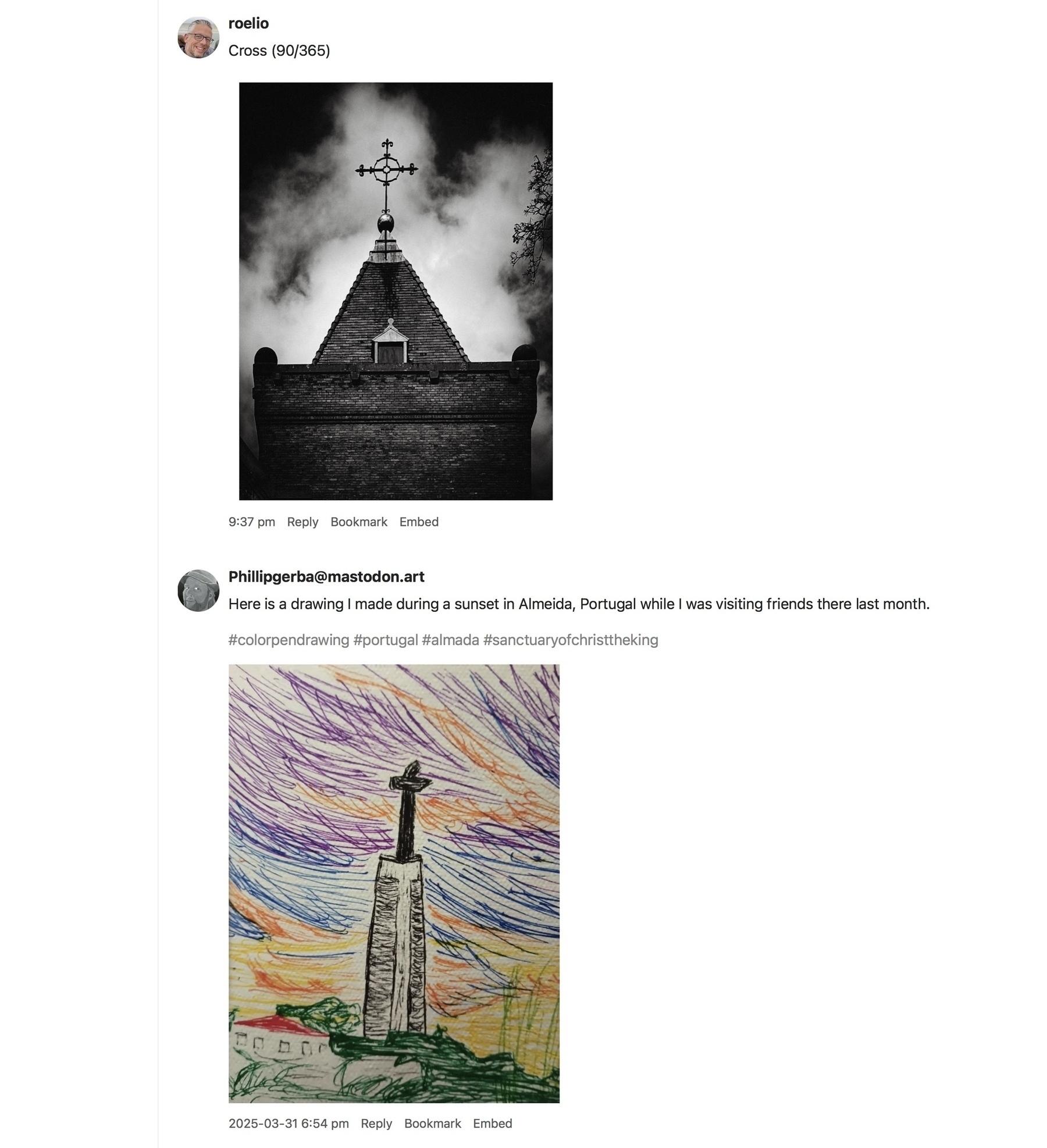
Great minds think alike in my timeline, by @roelio@micro.blog and @Phillipgerba@mastodon.art
-
The @pixeldailies.bsky.social #PixelDailies theme was #ladder Link has to climb the ultimate infinite ladder.

-
I suppose if you always play it safe (read: draw for more likes), you will never learn new things, and keep repeating old things until you’ve bored and stop creating. For me, this is a place of experimentation, finding your artistic limits, go beyond them, then dial back a bit.

-
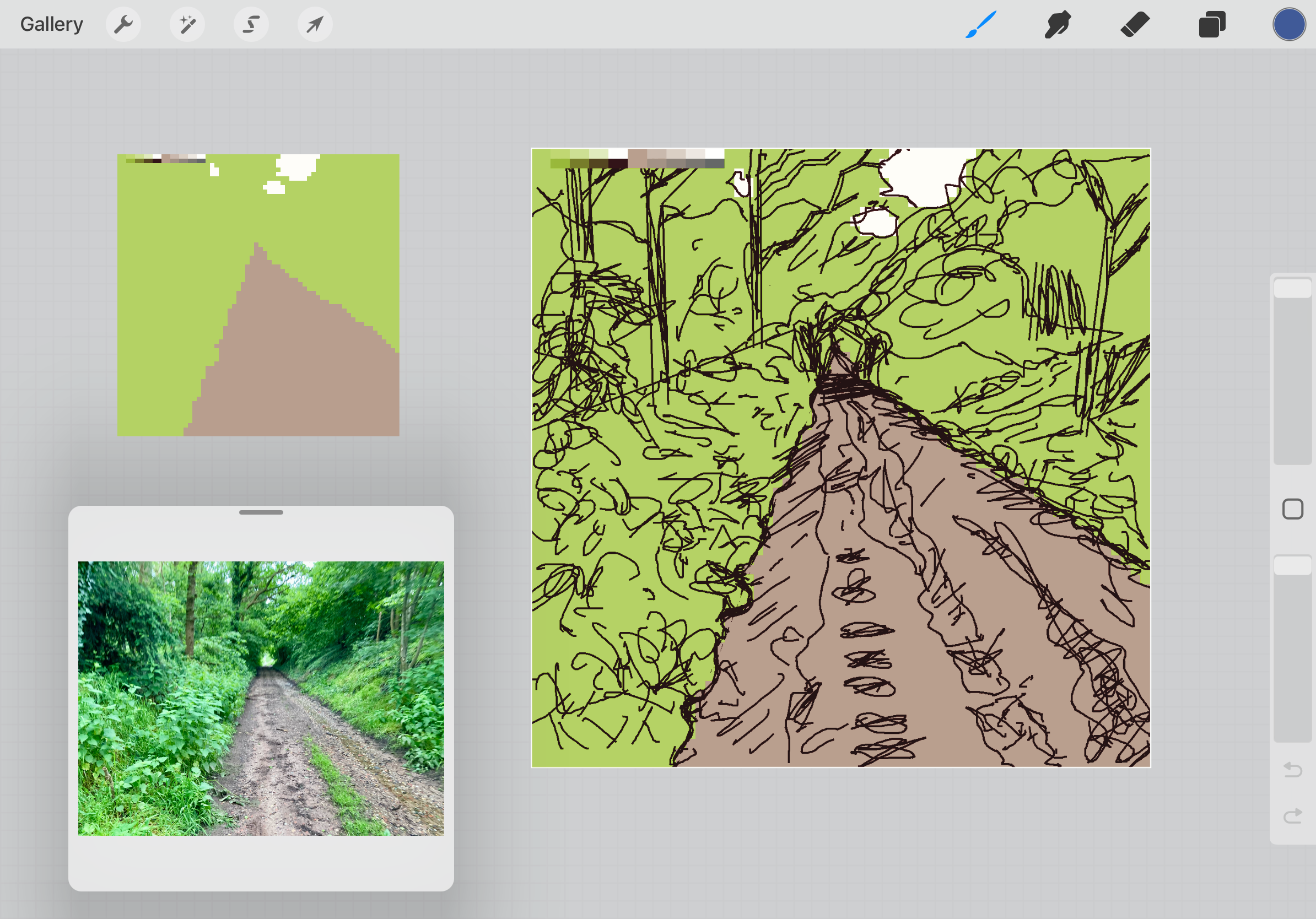
I started a new project in Procreate for pixel art. I already made a rough sketch and applied base colors (white, green and light-brown). It will become a 64 x 64 pixels piece for my Pixoo64. It’s been a while since I did a landscape, so it will be a challenge to finish it. Here’s a WIP.
-
Here’s the process video of the pixel portrait of Jean-Luc Picard.
-
I hand-made a pixel portrait of captain Jean-Luc Picard in Star Trek TNG, using Procreate.

-
I tweaked yesterday’s still pixel art thoroughly, so I think it got more “readable.” Next I did some simple animation, since that’s preferred, apparently, in the Divoom community.

-
Here’s the finished version of a baby enthusiastically holding a puppy.
