-
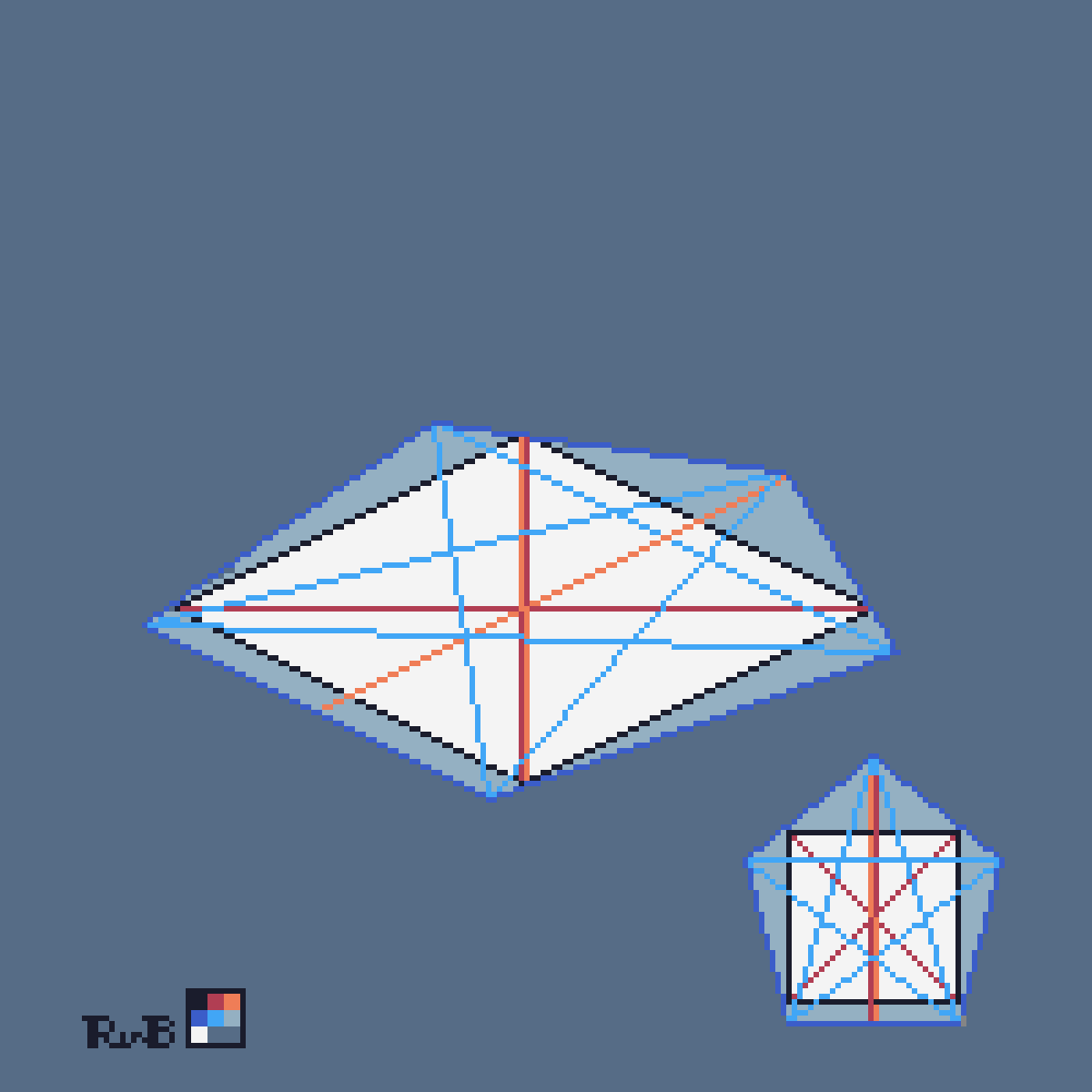
On YouTube I saw Matt Parker and Adam Savage do videos about how to construct geometric shapes in three dimensions. I tried the same with flat shapes in both 2D and (pixel art) isometric perspective. Since pixel art is a crude representation of reality, I had to fudge a lot to make it fit.
👾
-
Doing some character design in pixel art, Game Boy compatible.
👾
-
I drew a Bangladeshi girl in traditional dress based on this photo and an image search on traditional clothing from Bangladesh, which was rather sparse amongst the modern dresses inspired by tradition (because that what people might want to wear nowadays).
👾
-
I have today’s work cut out for me with this portrait of a Bangladeshi girl from 2011.
👾
-
Practicing dithering.
👾
-
I made this 64 by 64 pixel art portrait, referencing this photo of Raymond and using only four colors from the 2-bits-pips color palette.
👾
-
I did some work on my Dutch language running blog, and broke the site. Once I had repaired the damage, I permanently lost additional functionality (links to next and previous posts). You see, the service has changed, and my hack hadn’t kept up with the times. I guess the lesson is, use the default.
-
Drawn while listening to A Legacy of Biffs on The Incomparable Mothership podcast about Back to the Future 2. It’s an audio podcast, so I got to draw from imagination.
👾
-
I made this Game Boy compatible pixel art piece based on this excellent portrait.
👾
-
I tried drawing the same character in two different art styles, referencing a photo I took myself. The one on the right is (loosely) based on someone else’s art style.
👾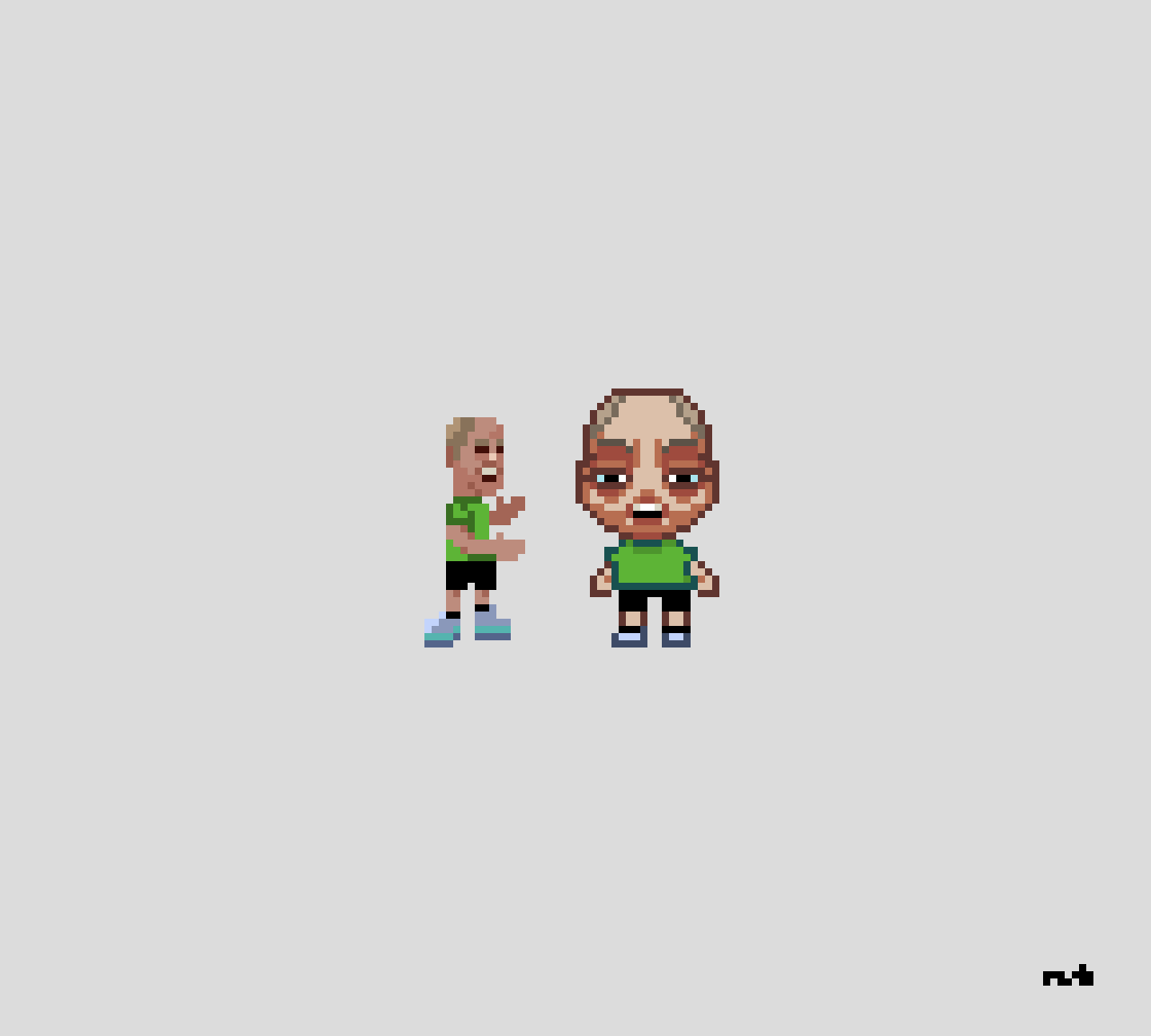
-
Oh boy, I need to learn about tilesets and game art to avoid attrocities like this one
👾💩
-
I tried to create an animated sprite of my cat. All I have to do now is give him a world to live in. That’s easy, right? 😂
👾
-
I wrote the previous post in the Strata app, shared the selected markdown text with Pythonista’s Preview Markdown to preview it, counted the characters with Word Counter Tool, then shared it with the Micro.blog app, and removed the
>before publishing. All done on an iPad with stage manager enabled 😅 -
This week I did three training sessions for running, two on a track, one on the road. While I’m recovering from an ankle injury, I have to keep the weekly mileage low, the tempos slow. My guess is that it’ll take until May before I’m back into my normal training regime of 60 km/week (37 mpw).

-
I used this photo as a reference for a small pixel art drawing of a deer. I tried to concentrate on clumps of pixels, but I see I need to study more to be effective. The shape’s okay-ish, which is an accomplishment at this scale, I think.
👾
-
The original Macintosh, aka 128K Mac, is often referred to as the computer that changed the world. It was the first commercially available computer with a graphical user interface. Pixel art for the Nintendo Game Boy screen (160 x 144 pixels, 4 shades of green).
👾
-
Sometimes you want your cat to play with their food. It keeps them happy if you surprise them once in a while by offering hidden food, so they’ll have to think how to get to it

-
I thought pixel animation would be easier. Alas, with iPadOS it still is too hard, so it seems, and Aseprite is still the desktop app to emulate. Yes, you can do animation on the iPad, but it takes a lot of time compared to what I’m used to on the desktop 20 years ago, using Moho.
👾

